Measuring and Explaining the Inter-Cluster Reliability of Multidimensional Projections

Hyeon Jeon, Hyung-Kwon Ko, Jaemin Jo, Youngtaek Kim, Jinwook Seo

External link (DOI)
View presentation:2021-10-27T18:15:00ZGMT-0600Change your timezone on the schedule page
2021-10-27T18:15:00Z
Exemplar figure, described by caption below
We propose Steadiness and Cohesiveness, two novel metrics to measure the inter-cluster reliability of multidimensional projection (MDP), specifically how well the inter-cluster structures are preserved between the original high-dimensional space and the low-dimensional projection space. Our metrics can also quantify pointwise distortions, allowing for the visualization of inter-cluster reliability in a projection, which we call a reliability map. This figure depicts the UMAP, Isomap, and LLE projections of the MNIST test dataset and the reliability maps that visualize each projection’s inter-cluster distortion, along with overall Steadiness (St) and Cohesiveness (Co) scores depicted under each technique.
Fast forward

Direct link to video on YouTube: https://youtu.be/EFaKO5hvtcw

Abstract

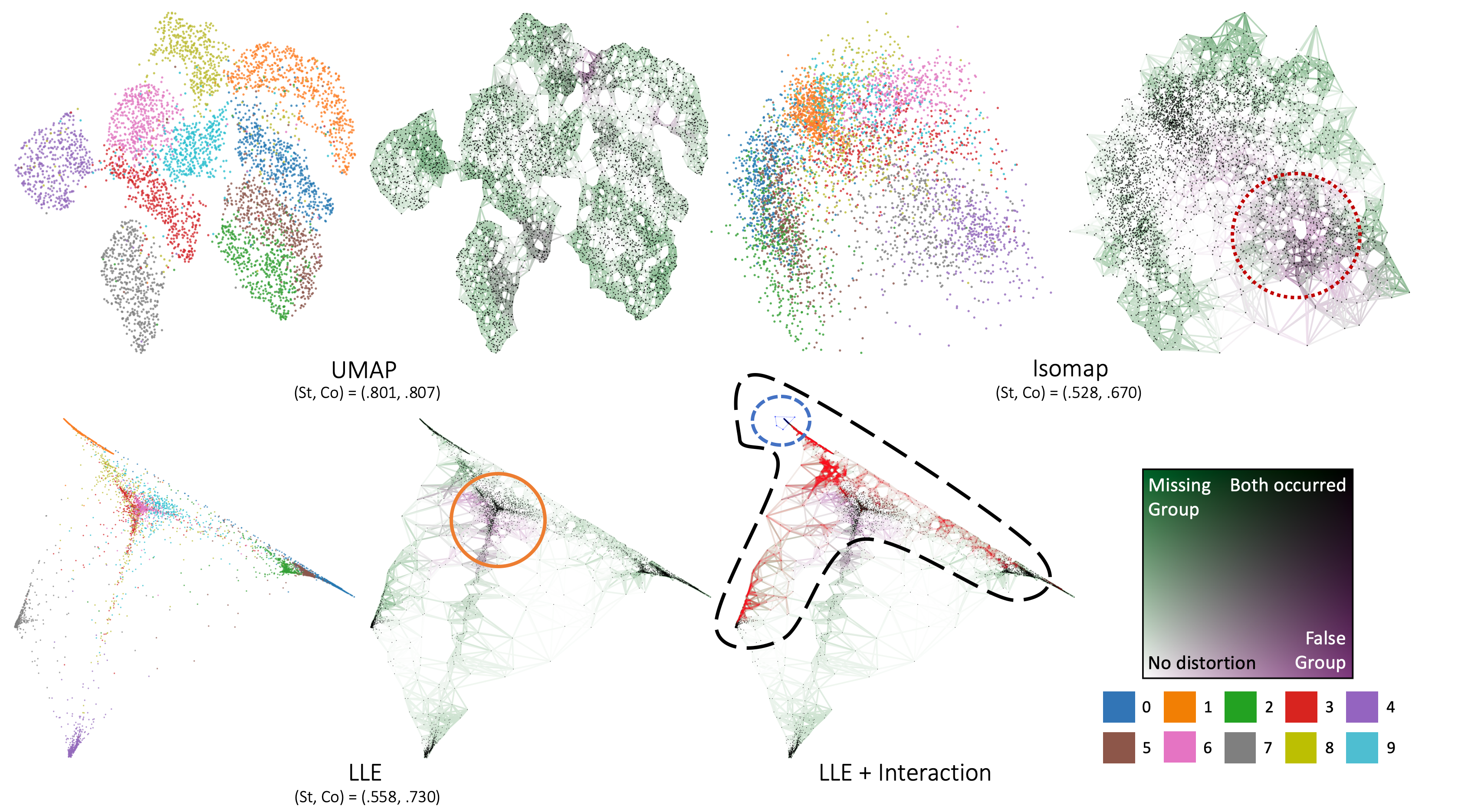
We propose Steadiness and Cohesiveness, two novel metrics to measure the inter-cluster reliability of multidimensional projection (MDP), specifically how well the inter-cluster structures are preserved between the original high-dimensional space and the low-dimensional projection space. Measuring inter-cluster reliability is crucial as it directly affects how well inter-cluster tasks (e.g., identifying cluster relationships in the original space from a projected view) can be conducted; however, despite the importance of inter-cluster tasks, we found that previous metrics, such as Trustworthiness and Continuity, fail to measure inter-cluster reliability. Our metrics consider two aspects of the inter-cluster reliability: Steadiness measures the extent to which clusters in the projected space form clusters in the original space, and Cohesiveness measures the opposite. They extract random clusters with arbitrary shapes and positions in one space and evaluate how much the clusters are stretched or dispersed in the other space. Furthermore, our metrics can quantify pointwise distortions, allowing for the visualization of inter-cluster reliability in a projection, which we call a reliability map. Through quantitative experiments, we verify that our metrics precisely capture the distortions that harm inter-cluster reliability while previous metrics have difficulty capturing the distortions. A case study also demonstrates that our metrics and the reliability map 1) support users in selecting the proper projection techniques or hyperparameters and 2) prevent misinterpretation while performing inter-cluster tasks, thus allow an adequate identification of inter-cluster structure.