Edge-Path Bundling: A Less Ambiguous Edge Bundling Approach
Markus Wallinger, Daniel Archambault, David Auber, Martin Nöllenburg, Jaakko Peltonen
External link (DOI)
View presentation:2021-10-28T17:45:00ZGMT-0600Change your timezone on the schedule page
2021-10-28T17:45:00Z
Fast forward
Direct link to video on YouTube: https://youtu.be/3NHfrXpS2IU
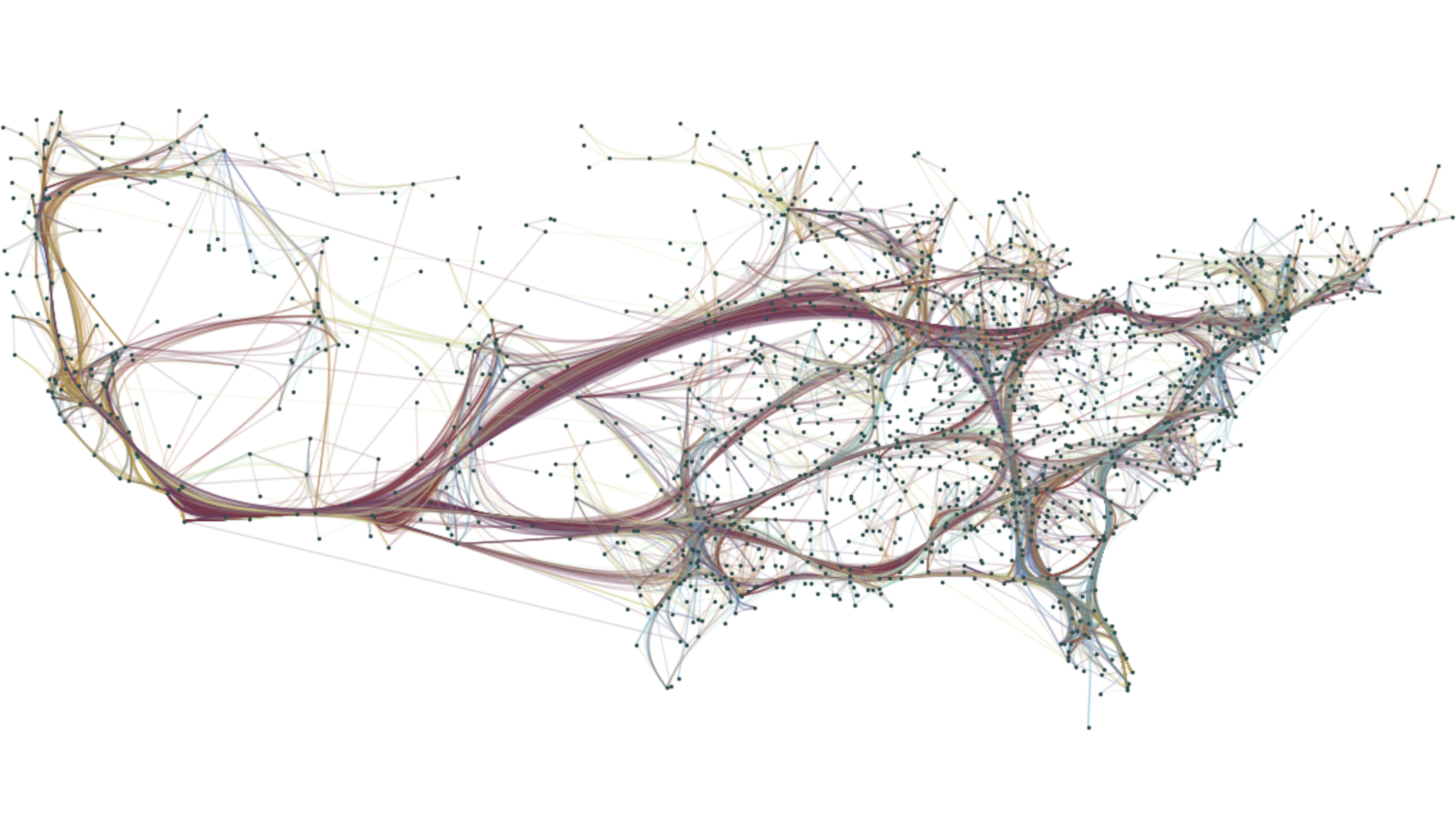
Abstract
Edge bundling techniques cluster edges with similar attributes (i.e. similarity in direction and proximity) together to reduce the visual clutter. All edge bundling techniques to date implicitly or explicitly cluster groups of individual edges, or parts of them, together based on these attributes. These clusters can result in ambiguous connections that do not exist in the data. Confluent drawings of networks do not have these ambiguities, but require the layout to be computed as part of the bundling process. We devise a new bundling method, edge-path bundling, to simplify edge clutter while greatly reducing ambiguities compared to previous bundling techniques. Edge-path bundling takes a layout as input and clusters each edge along a weighted, shortest path to limit its deviation from a straight line. Edge-path bundling does not incur independent edge ambiguities typically seen in all edge bundling methods, and the level of bundling can be tuned through shortest path distances, Euclidean distances, and combinations of the two. Also, directed edge bundling naturally emerges from the model. Through metric evaluations, we demonstrate the advantages of edge-path bundling over other techniques.