Honorable Mention

Interactive Exploration of Physically-Observable Objective Vortices in Unsteady 2D Flow

Xingdi Zhang, Markus Hadwiger, Thomas Theussl, Peter Rautek

External link (DOI)
View presentation:2021-10-27T13:45:00ZGMT-0600Change your timezone on the schedule page
2021-10-27T13:45:00Z
Exemplar figure, described by caption below
We show six different observer-relative visualizations of the same unsteady 2D input flow field, with respect to six different observers (vertical axes correspond to time). Each visualization is relative to a specific physically-realizable observer, depicted via an observer world line in each inset. Different vortex structures become visible relative to different observers, with colors and opacities encoding the coherence of path lines. Our interactive framework enables smoothly choosing, interpolating, and averaging observers, leading to smoothly changing observer-relative visualizations.
Fast forward

Direct link to video on YouTube: https://youtu.be/0kdWTHGd5yQ

Abstract

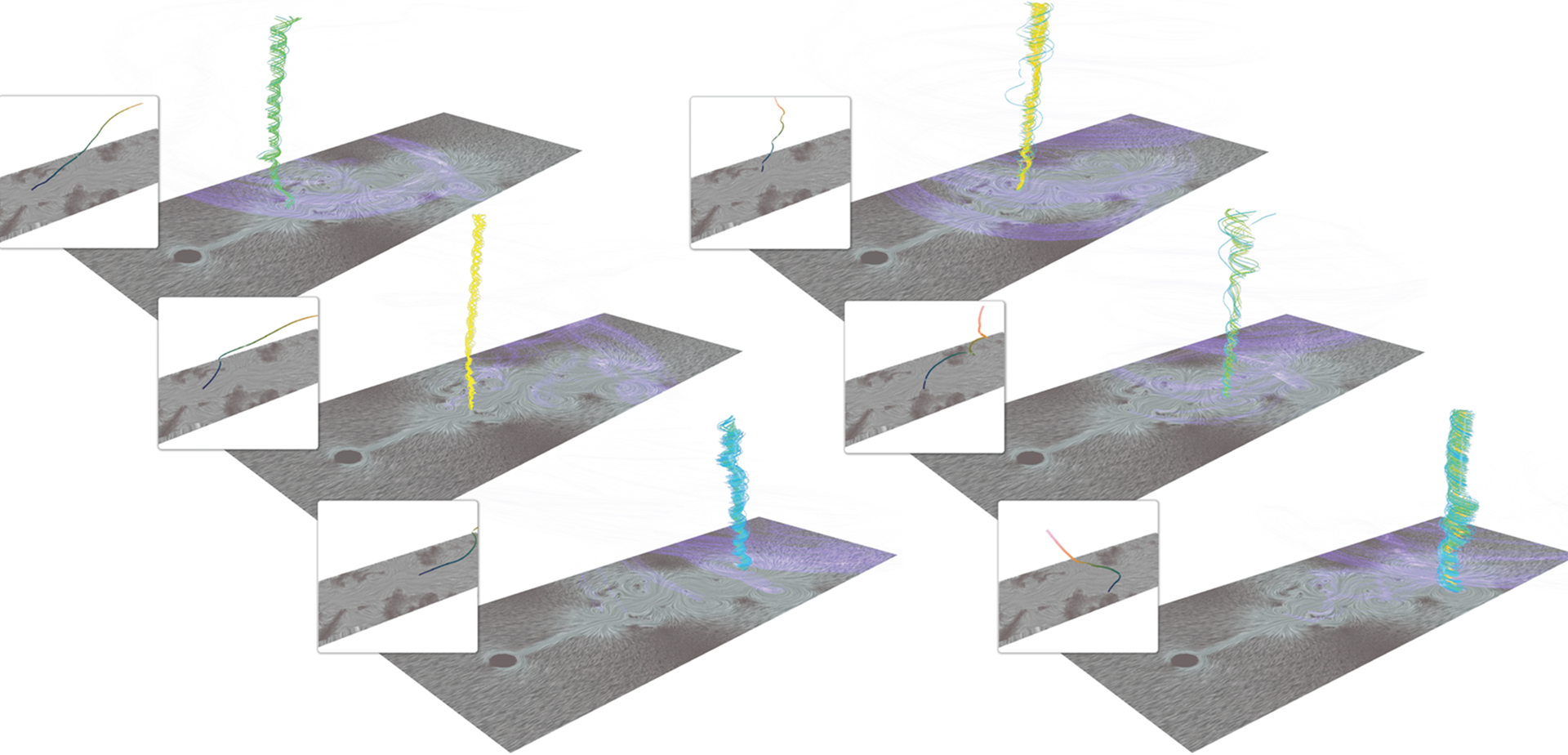
State-of-the-art computation and visualization of vortices in unsteady fluid flow employ objective vortex criteria, which makes them independent of reference frames or observers. However, objectivity by itself, although crucial, is not sufficient to guarantee that one can identify physically-realizable observers that would perceive or detect the same vortices. Moreover, a significant challenge is that a single reference frame is often not sufficient to accurately observe multiple vortices that follow different motions. This paper presents a novel framework for the exploration and use of an interactively-chosen set of observers, of the resulting relative velocity fields, and of objective vortex structures. We show that our approach facilitates the objective detection and visualization of vortices relative to well-adapted reference frame motions, while at the same time guaranteeing that these observers are in fact physically realizable. In order to represent and manipulate observers efficiently, we make use of the low-dimensional vector space structure of the Lie algebra of physically-realizable observer motions. We illustrate that our framework facilitates the efficient choice and guided exploration of objective vortices in unsteady 2D flow, on planar as well as on spherical domains, using well-adapted reference frames.