Uncertainty Visualization of 2D Morse Complex Ensembles Using Statistical Summary Maps



Tushar Athawale, Dan Maljovec, Lin Yan, Chris R. Johnson, Valerio Pascucci, Bei Wang

 External link (DOI) 

 View presentation:2020-10-28T18:15:00ZGMT-0600Change your timezone on the schedule page
2020-10-28T18:15:00Z

Exemplar figure — The image in the leftmost column depicts an input ensemble of 2D Morse complexes. The uncertainty in gradient flows, and hence the Morse complexes, across the input ensemble is then quantified and visualized using our proposed statistical summary maps, i.e., the probabilistic map, significance map, and survival map.

Fast forward

Direct link to video on YouTube: https://youtu.be/V5XkB72A4C0

Keywords

Morse complexes, uncertainty visualization, topological data analysis

Abstract

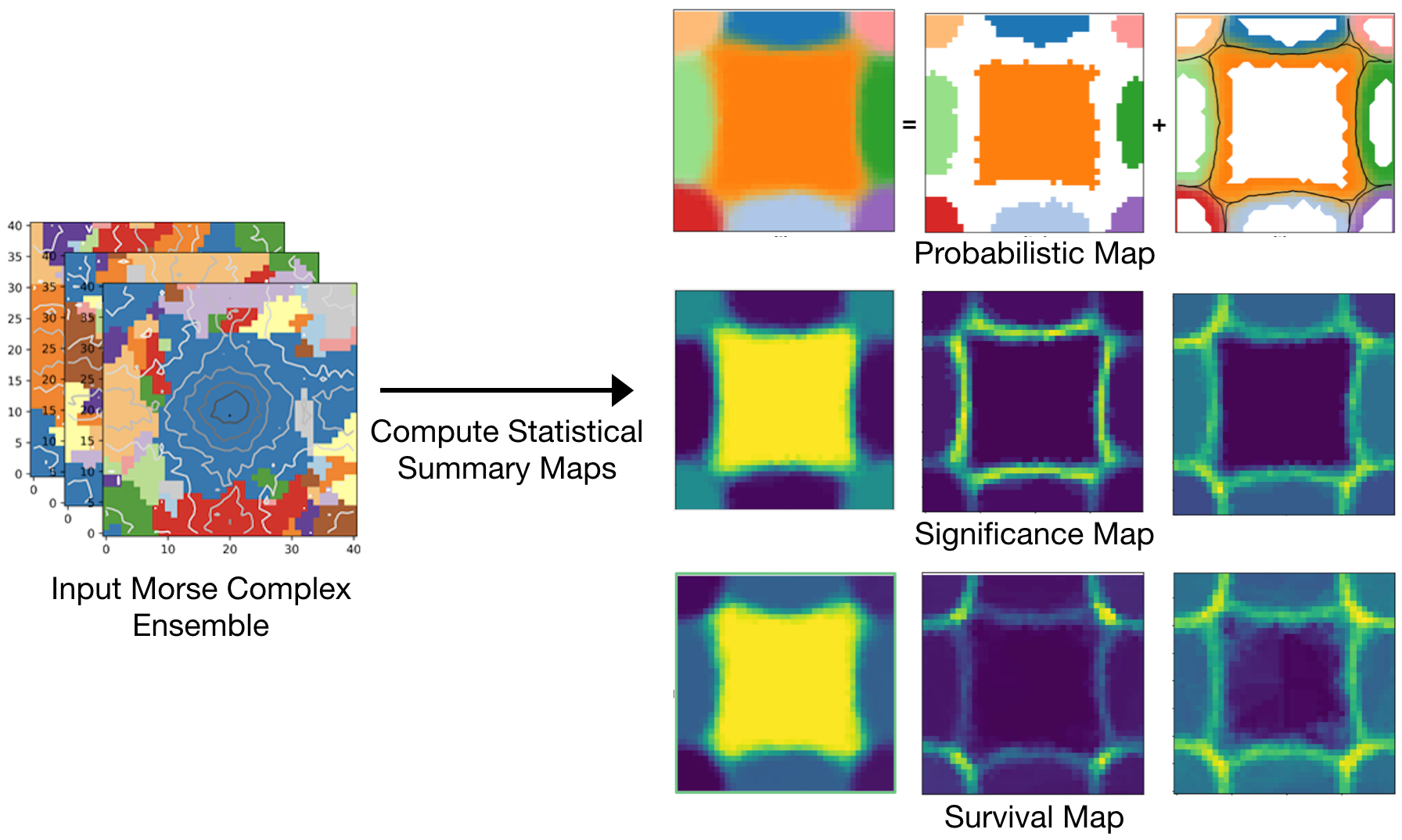
Morse complexes are gradient-based topological descriptors with close connections to Morse theory. They are widely applicable in scientific visualization as they serve as important abstractions for gaining insights into the topology of scalar fields. Data uncertainty inherent to scalar fields due to randomness in their acquisition and processing, however, limits our understanding of Morse complexes as structural abstractions. We, therefore, explore uncertainty visualization of an ensemble of 2D Morse complexes that arises from scalar fields coupled with data uncertainty. We propose statistical summary maps as new entities for quantifying structural variations and visualizing positional uncertainties of Morse complexes in ensembles. Specifically, we introduce three types of statistical summary maps – the probabilistic map, the significance map, and the survival map – to characterize the uncertain behaviors of gradient flows. We demonstrate the utility of our proposed approach using wind, flow, and ocean eddy simulation datasets.