A Domain-Oblivious Approach for Learning Concise Representations of Filtered Topological Spaces for Clustering

Fast forward

Direct link to video on YouTube: https://youtu.be/7uGtGV1G7qc

Keywords

Topological data analysis, Persistence diagrams, Persistence diagram distances, Learned hashing, Clustering

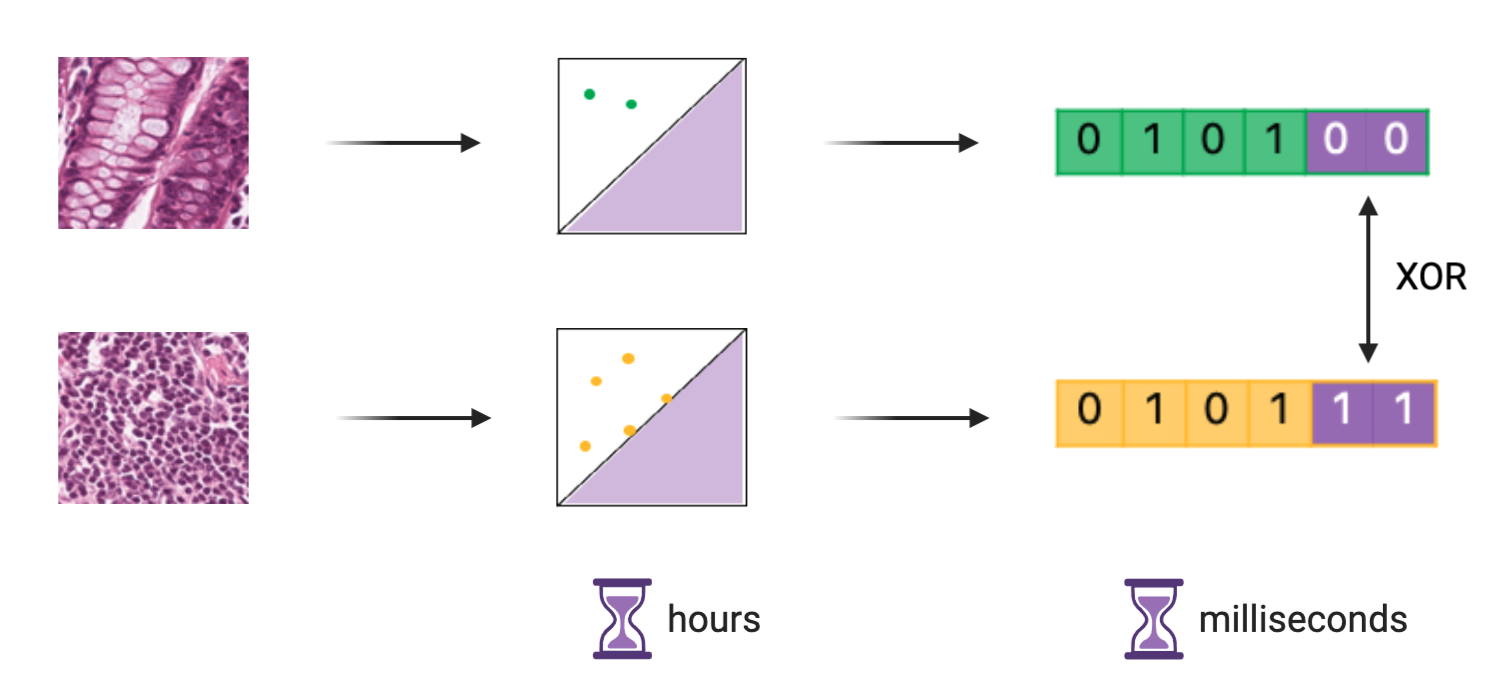
Abstract

Persistence diagrams have been widely used to quantify the underlying features of filtered topological spaces in data visualization. In many applications, computing distances between diagrams is essential; however, computing these distances has been challenging due to the computational cost. In this paper, we propose a persistence diagram hashing framework that learns a binary code representation of persistence diagrams, which allows for fast computation of distances. This framework is built upon a generative adversarial network (GAN) with a diagram distance loss function to steer the learning process. Instead of using standard representations, we hash diagrams into binary codes, which have natural advantages in large-scale tasks. The training of this model is domain-oblivious in that it can be computed purely from synthetic, randomly created diagrams. As a consequence, our proposed method is directly applicable to various datasets without the need for retraining the model. These binary codes, when compared using fast Hamming distance, better maintain topological similarity properties between datasets than other vectorized representations. To evaluate this method, we apply our framework to the problem of diagram clustering and we compare the quality and performance of our approach to the state-of-the-art. In addition, we show the scalability of our approach on a dataset with 10k persistence diagrams, which is not possible with current techniques. Moreover, our experimental results demonstrate that our method is significantly faster with the potential of less memory usage, while retaining comparable or better quality comparisons.