Joint t-SNE for Comparable Projections of Multiple High-Dimensional Datasets

Yinqiao Wang, Lu Chen, Jaemin Jo, Yunhai Wang

External link (DOI)
View presentation:2021-10-29T16:00:00ZGMT-0600Change your timezone on the schedule page
2021-10-29T16:00:00Z
Exemplar figure, described by caption below
Comparison of the 5-Gaussian dataset projection of four different t-SNE methods. a) t-SNE produced misaligned layouts all across four time frames. b) Equal-initialization t-SNE provides better visual consistency than t-SNE but there are still unnecessary movements of clusters. c) Dynamic t-SNE showed smoothing effect by distorting projections at t = 2 and 3. d) Joint t-SNE generated coherent and reliable projections that reflected the ground-truth transformations of clusters.
Fast forward

Direct link to video on YouTube: https://youtu.be/6Gxdv-unloM

Abstract

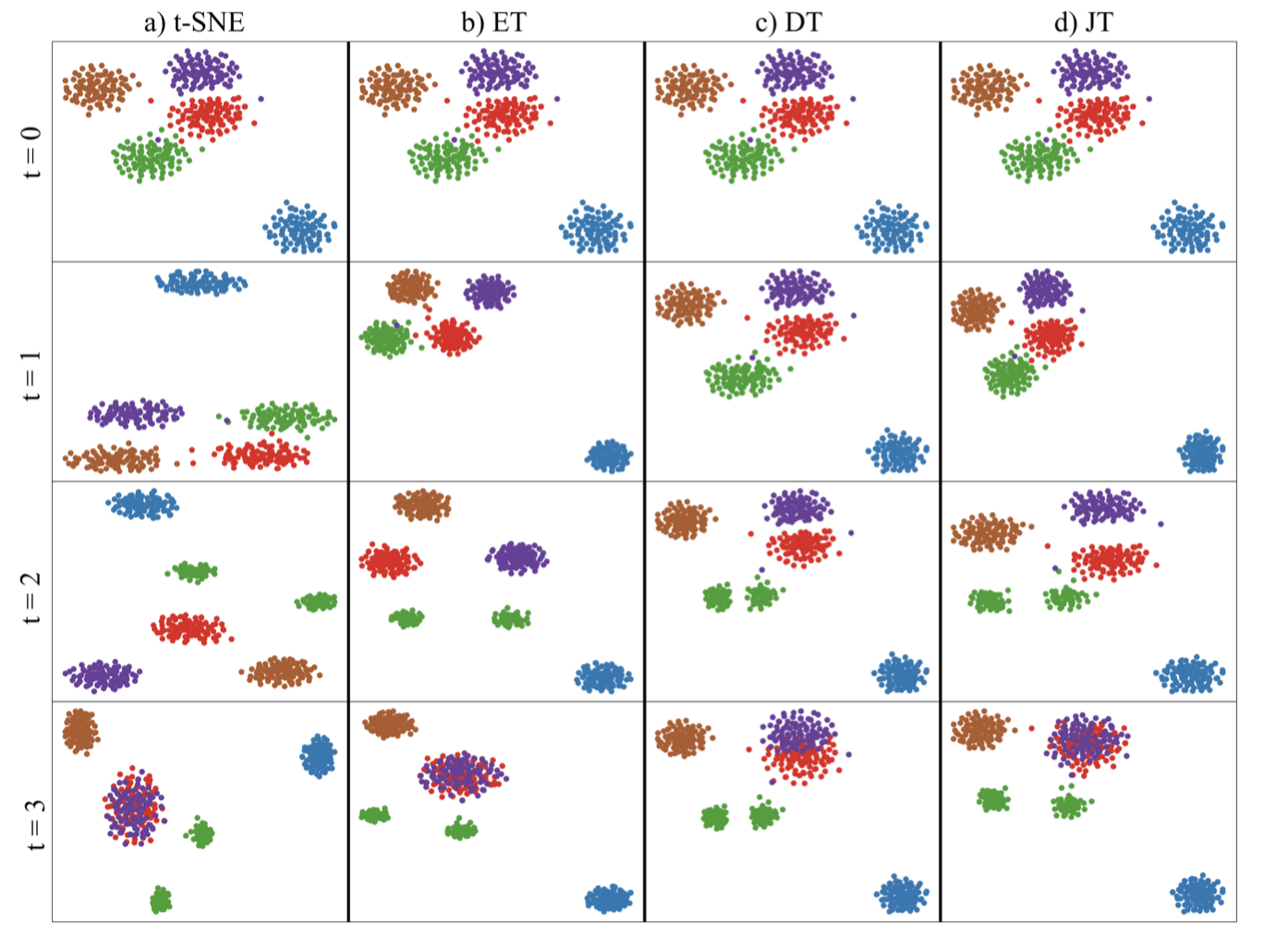
We present Joint t-Stochastic Neighbor Embedding (Joint t-SNE), a technique to generate comparable projections of multiple high-dimensional datasets. Although t-SNE has been widely employed to visualize high-dimensional datasets from various domains, it is limited to projecting a single dataset. When a series of high-dimensional datasets, such as datasets changing over time, is projected independently using t-SNE, misaligned layouts are obtained. Even items with identical features across datasets are projected to different locations, making the technique unsuitable for comparison tasks. To tackle this problem, we introduce edge similarity, which captures the similarities between two adjacent time frames based on the Graphlet Frequency Distribution (GFD). We then integrate a novel loss term into the t-SNE loss function, which we call vector constraints, to preserve the vectors between projected points across the projections, allowing these points to serve as visual landmarks for direct comparisons between projections. Using synthetic datasets whose ground-truth structures are known, we show that Joint t-SNE outperforms existing techniques, including Dynamic t-SNE, in terms of local coherence error, Kullback-Leibler divergence, and neighborhood preservation. We also showcase a real-world use case to visualize and compare the activation of different layers of a neural network.