Towards Adaptive Refinement for Multivariate Functional Approximation of Scientific Data

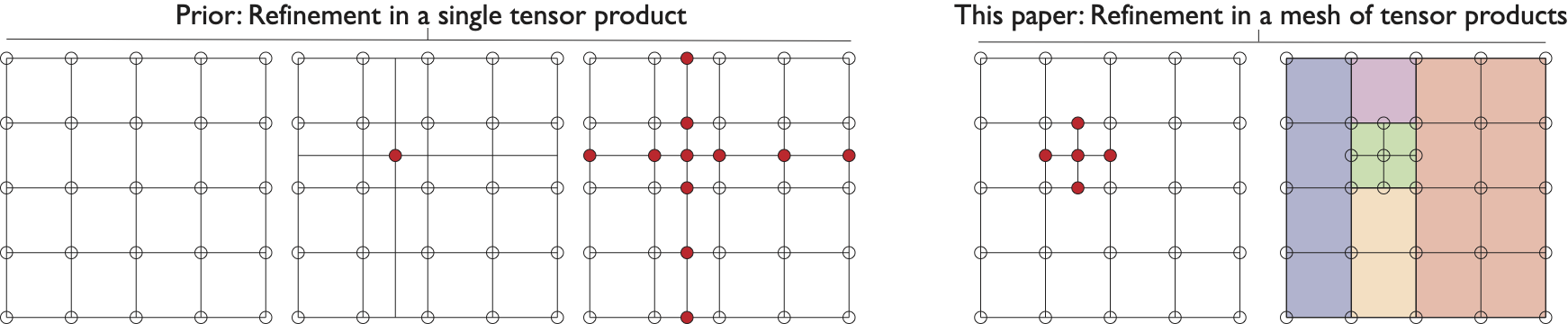
Abstract

We investigate a data model for adaptive refinement in multivariate functional approximation of scientific data, based on a mesh of varying-resolution tensor products, and offering reduced size compared with a single tensor product representation. The mesh of tensor products adjoins in irregular fashion to tessellate the entire domain, with high-degree continuity across tensor product boundaries. The result is that regions of refinement, with additional knots and control points, are localized to individual tensor products rather than extending throughout the entire domain. The model attains similar accuracy with fewer total control points than a single tensor product model, at the cost of added computational complexity to manage the continuity and accuracy across tensor products. We describe our high-dimensional data organization and demonstrate how to approximate scientific datasets using our data model. Size and speed are compared between a single tensor product and our representation. Initial results demonstrate correct functionality and modest reduction in the number of control points required to attain comparable accuracy as a single tensor, with increased computation time as expected. Our initial findings indicate two avenues for future research: additional tuning of the adaptive refinement algorithm to reduce size further, and accelerating computation through parallelism.