Global Topology of 3D Symmetric Tensor Fields

Fast forward

Full Video

Keywords

Tensor field visualization, 3D symmetric tensor fields, global tensor field topology, topological graphs, degenerate curves, neutral surfaces, wedges and trisectors

Abstract

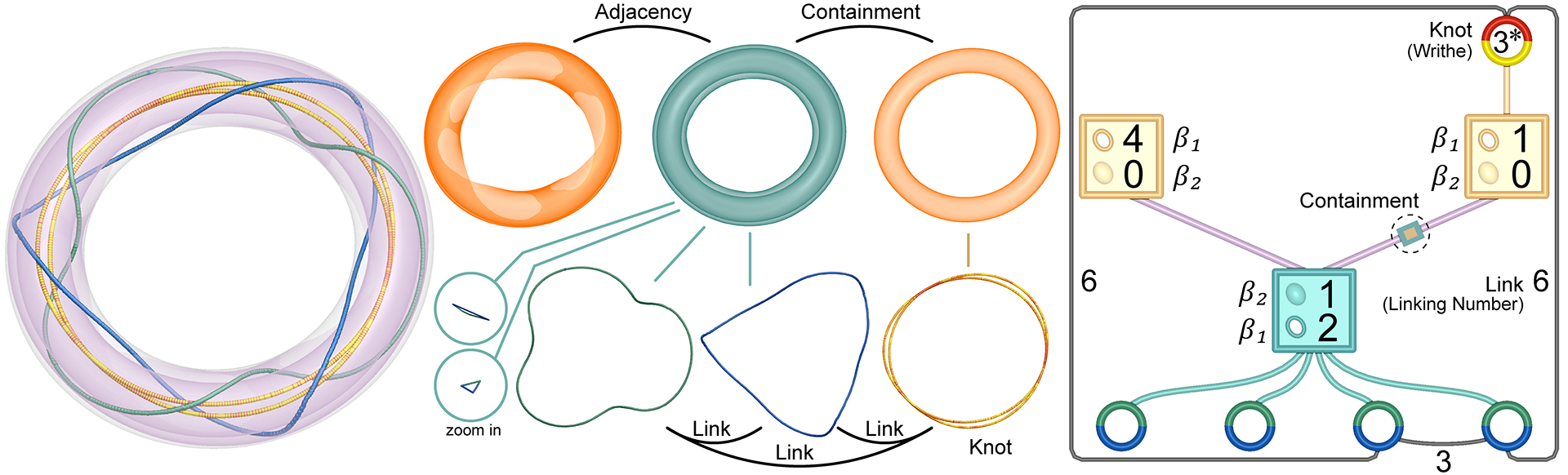
There have been recent advances in the analysis and visualization of 3D symmetric tensor fields, with a focus on the robust extraction of tensor field topology. However, topological features such as degenerate curves and neutral surfaces do not live in isolation. Instead, they intriguingly interact with each other. In this paper, we introduce the notion of {\em topological graph} for 3D symmetric tensor fields to facilitate global topological analysis of such fields. The nodes of the graph include degenerate curves and regions bounded by neutral surfaces in the domain. The edges in the graph denote the adjacency information between the regions and degenerate curves. In addition, we observe that a degenerate curve can be a loop and even a knot and that two degenerate curves (whether in the same region or not) can form a link. We provide a definition and theoretical analysis of individual degenerate curves in order to help understand why knots and links may occur. Moreover, we differentiate between wedges and trisectors, thus making the analysis more detailed about degenerate curves. We incorporate this information into the topological graph. Such a graph can not only reveal the global structure in a 3D symmetric tensor field but also allow two symmetric tensor fields to be compared. We demonstrate our approach by applying it to solid mechanics and material science data sets.