ExTreeM: Scalable Augmented Merge Tree Computation via Extremum Graphs

Jonas Lukasczyk, Michael Will, Florian Wetzels, Gunther H Weber, Christoph Garth

DOI: 10.1109/TVCG.2023.3326526

Room: 106

2023-10-26T03:48:00ZGMT-0600Change your timezone on the schedule page
2023-10-26T03:48:00Z
Exemplar figure, described by caption below
Merge trees are fundamental data abstractions of scalar field topology that record at which scalar values superlevel set components appear and merge. They can be used for a plethora of visualization and analysis task such as data segmentation (top). We present ExTreeM, a generic schema using the ascending / descending manifold to generate a smaller extremum graph of the dataset (bottom, middle) and a specialized merge tree algorithm (bottom, right) showing speedups of up to one order of magnitude over the current state of the art.
Fast forward
Full Video
Keywords

Scalar field topology, merge trees, persistence pairs, high performance computing.

Abstract

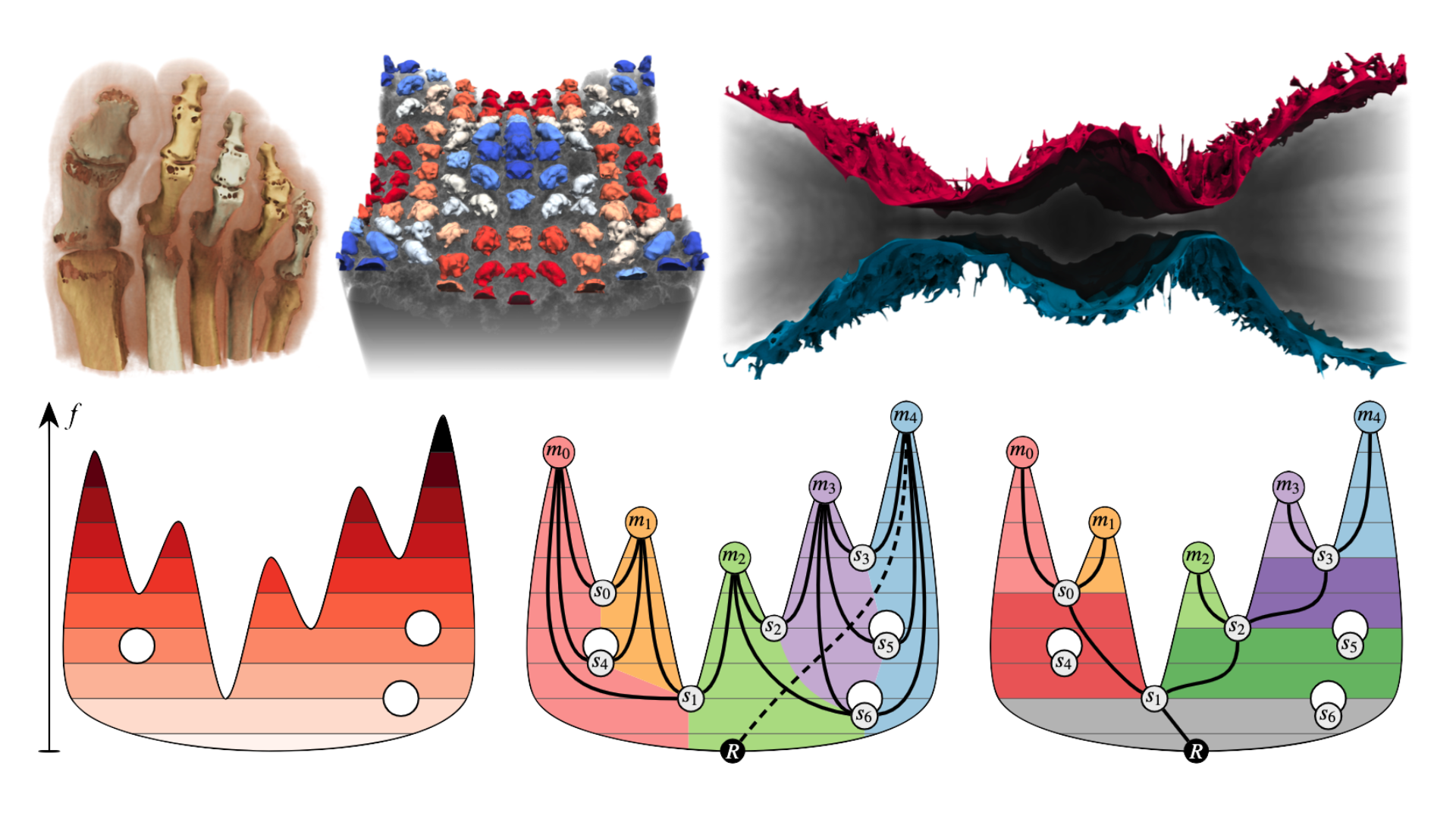
Over the last decade merge trees have been proven to support a plethora of visualization and analysis tasks since they effectively abstract complex datasets. This paper describes the ExTreeM-Algorithm: a scalable algorithm for the computation of merge trees via extremum graphs. The core idea of ExTreeM is to first derive the extremum graph G of an input scalar field f defined on a cell complex K, and subsequently compute the unaugmented merge tree of f on G instead of K; which are equivalent. Any merge tree algorithm can be carried out significantly faster on G, since K in general contains substantially more cells than G. To further speed up computation, ExTreeM includes a tailored procedure to derive merge trees of extremum graphs. The computation of the fully augmented merge tree, i.e., a merge tree domain segmentation of K, can then be performed in an optional post processing step. All steps of ExTreeM consist of procedures with high parallel efficiency, and we provide a formal proof of its correctness. Our experiments, performed on publicly available datasets, report a speedup of up to one order of magnitude over the state-of-the-art algorithms included in the TTK and VTK-m software libraries, while also requiring significantly less memory and exhibiting superior scaling behavior.