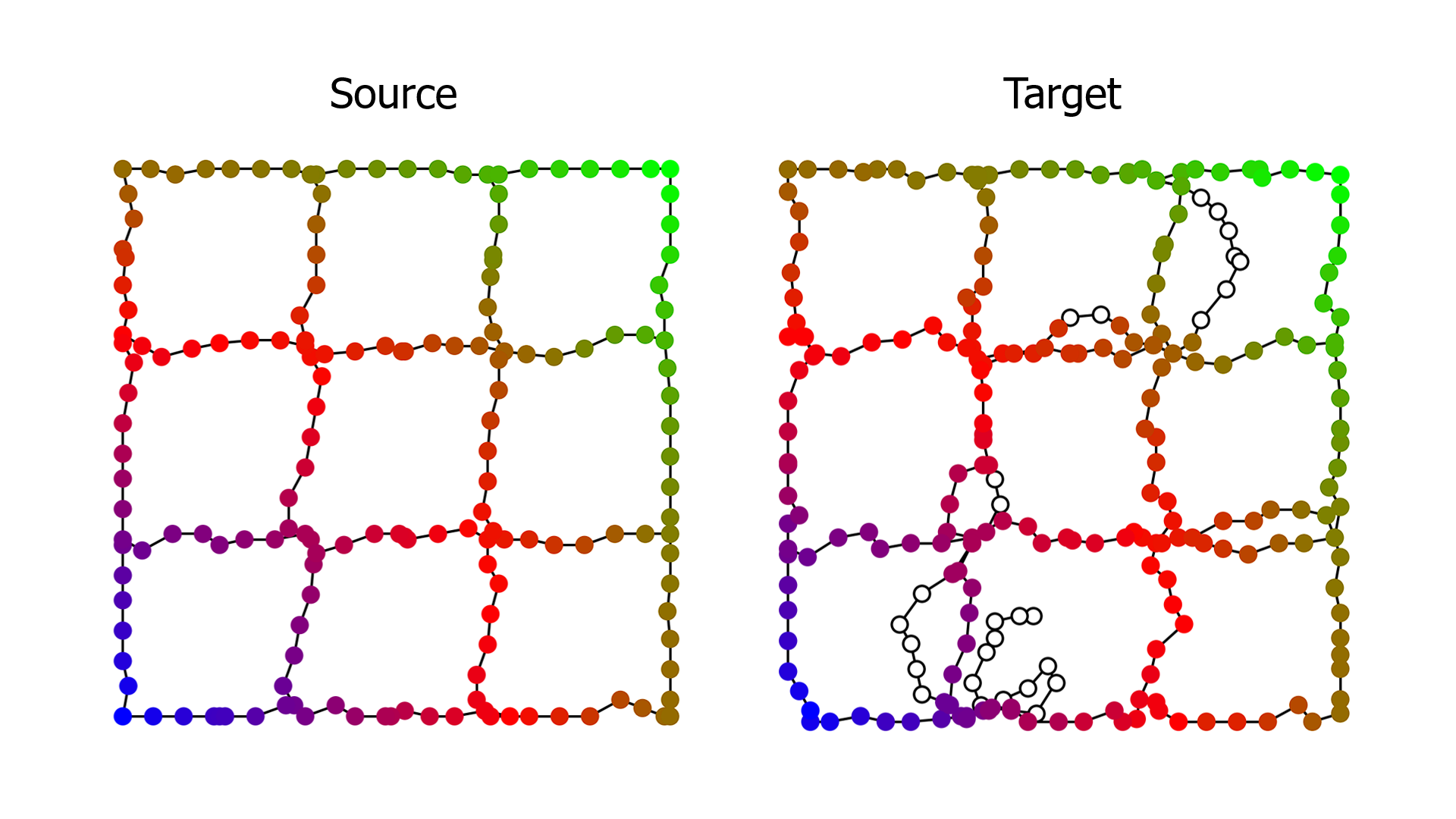
Comparing Morse Complexes Using Optimal Transport: An Experimental Study



Mingzhe Li, Carson Storm, Austin Yang Li, Tom Needham, Bei Wang Phillips

 Room: 104

2023-10-24T23:03:00ZGMT-0600Change your timezone on the schedule page
2023-10-24T23:03:00Z

Exemplar figure, described by caption below — The source and the target networks are generated from Morse graphs. The color correspondence indicates structural alignments between the source and the target using the partial Fused Gromov-Wasserstein distance. Noisy features that are ignored in the alignment are shown as hollow circles.

Fast forward

Full Video

Keywords

Morse Complexes, topological data analysis, optimal transport, topology in visualization

Abstract

Morse complexes and Morse-Smale complexes are topological descriptors popular in topology-based visualization. Comparing these complexes plays an important role in their applications in feature correspondences, feature tracking, symmetry detection, and uncertainty visualization. Leveraging recent advances in optimal transport, we apply a class of optimal transport distances to the comparative analysis of Morse complexes. Contrasting with existing comparative measures, such distances are easy and efficient to compute, and naturally provide structural matching between Morse complexes. We perform an experimental study involving scientific simulation datasets and discuss the effectiveness of these distances as comparative measures for Morse complexes. We also provide an initial guideline for choosing the optimal transport distances under various data assumptions.