Visualizing Topological Importance: A Class-Driven Approach

Yu Qin, Brittany Terese Fasy, Carola Wenk, Brian Summa

Room: 106

2023-10-22T03:00:00ZGMT-0600Change your timezone on the schedule page
2023-10-22T03:00:00Z
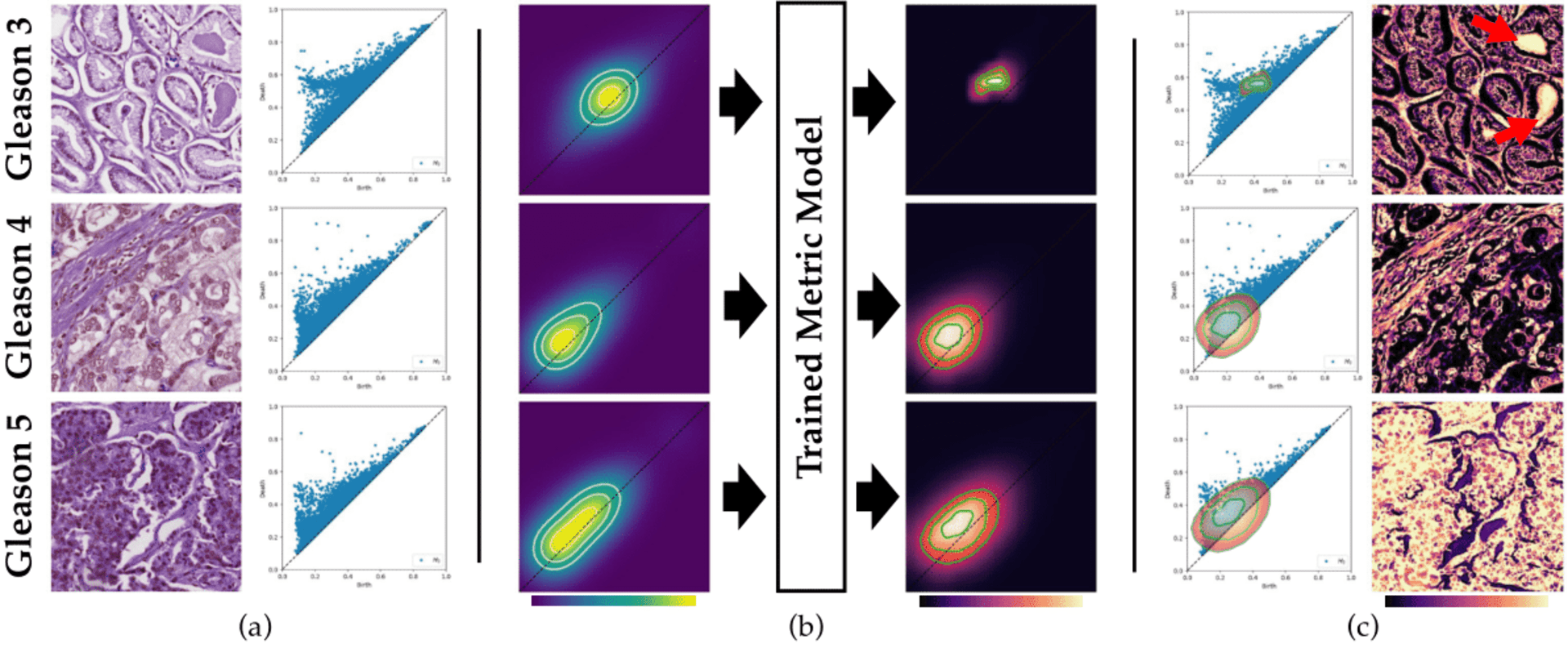
Exemplar figure, described by caption below
(a) A common task in topological data analysis: extracting a persistence diagram of topological features. In this case, features are based on the sublevel set filtration of pathology images with class labels (Gleason grade) that define the progression of prostate cancer~\cite{lawson2019persistent}. Knowing which features are important for each class is commonly an educated guess with the lifetime of a feature (persistence) often assumed to define importance. (b) Our approach, based on a learned metric classifier, takes as input the unweighted density of persistence points and reweighs this density based on what best defines a class. This allows us to build a field of importance for regions of a diagram. (c) This importance field can be used to create visualizations to illuminate which features drive a classification. For example, it can highlight what points are important directly in a diagram or, in the case of sublevel set filtrations, visualize the important structure directly in an image. Consider that a hallmark of prostate cancer is gland degeneration as the disease progresses. Calcifications (red arrow) are only present in well-structured glands and are highlighted as important structures for Gleason 3, an earlier stage of the disease.
Abstract

This paper presents the first approach to visualize the importance of topological features that define classes of data. Topological features, with their ability to abstract the fundamental structure of complex data, are an integral component of visualization and analysis pipelines. Although not all topological features present in data are of equal importance. To date, the default definition of feature importance is often assumed and fixed. This work shows how proven explainable deep learning approaches can be adapted for use in topological classification. In doing so, it provides the first technique that illuminates what topological structures are important in each dataset in regards to their class label. In particular, the approach uses a learned metric classifier with a density estimator of the points of a persistence diagram as input. This metric learns how to reweigh this density such that classification accuracy is high. By extracting this weight, an importance field on persistent point density can be created. This provides an intuitive representation of persistence point importance that can be used to drive new visualizations. This work provides two examples: Visualization on each diagram directly and, in the case of sublevel set filtrations on images, directly on the images themselves. This work highlights real-world examples of this approach visualizing the important topological features in graph, 3D shape, and medical image data.