Taming Horizontal Instability in Merge Trees: On the Computation of a Comprehensive Deformation-based Edit Distance
Florian Wetzels, Markus Anders, Christoph Garth
Room: 106
2023-10-22T03:00:00ZGMT-0600Change your timezone on the schedule page
2023-10-22T03:00:00Z
Full Video
Abstract
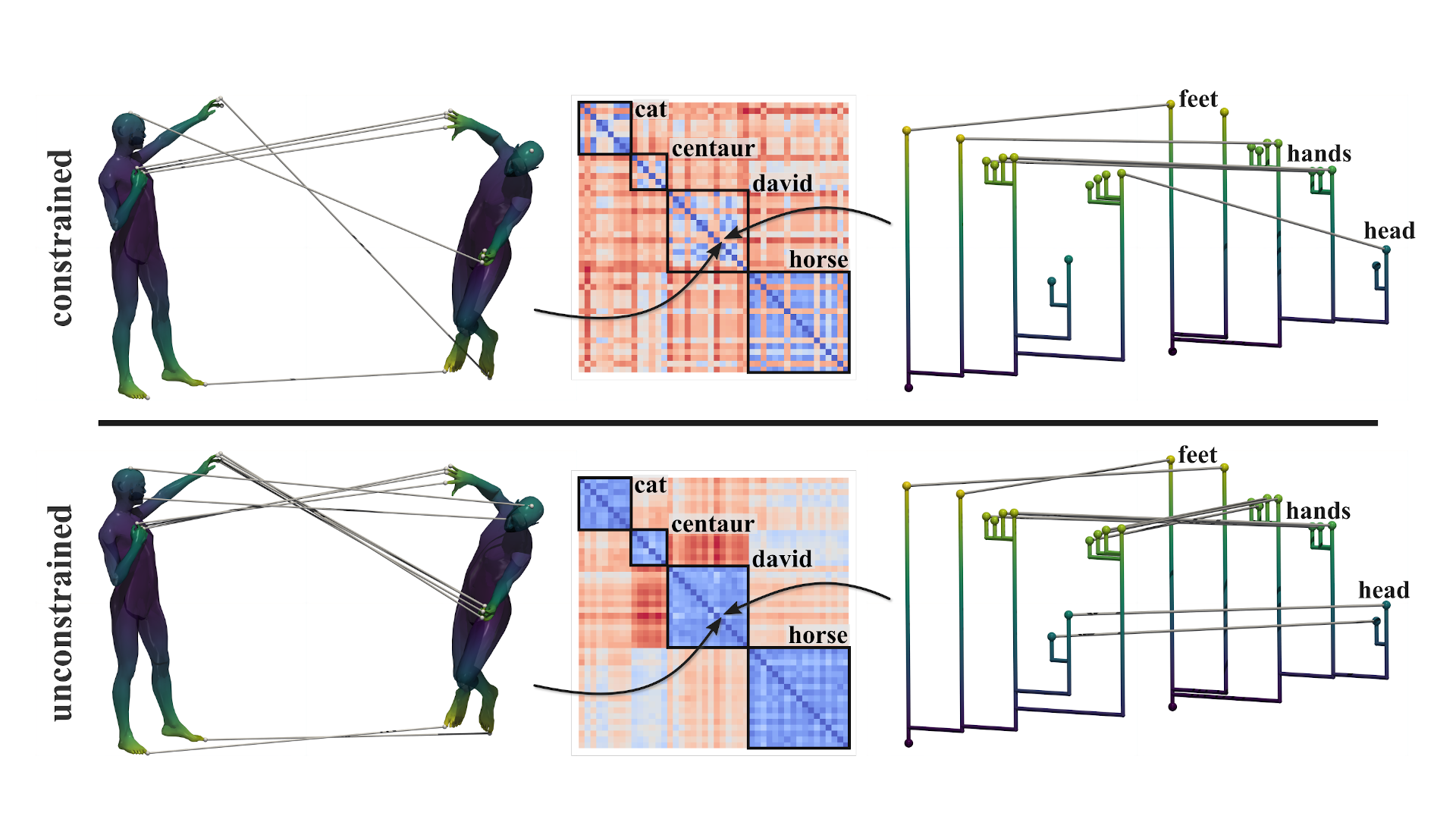
Comparative analysis of scalar fields in scientific visualization often involves distance functions on topological abstractions. This paper focuses on the merge tree abstraction (representing the nesting of sub- or superlevel sets) and proposes the application of the unconstrained deformation-based edit distance. Previous approaches on merge trees often suffer from instability: small perturbations in the data can lead to large distances of the abstractions. While some existing methods can handle so-called vertical instability, the unconstrained deformation-based edit distance addresses both vertical and horizontal instabilities, also called saddle swaps. We establish the computational complexity as NP-complete, and provide an integer linear program formulation for computation. Experimental results on the TOSCA shape matching ensemble provide evidence for the stability of the proposed distance. We thereby showcase the potential of handling saddle swaps for comparison of scalar fields through merge trees.