A Mathematical Foundation for the Spatial Uncertainty of Critical Points in Probabilistic Scalar Fields
Dominik Vietinghoff, Michael Böttinger, Gerik Scheuermann, Christian Heine
Room: 106
2023-10-22T03:00:00ZGMT-0600Change your timezone on the schedule page
2023-10-22T03:00:00Z
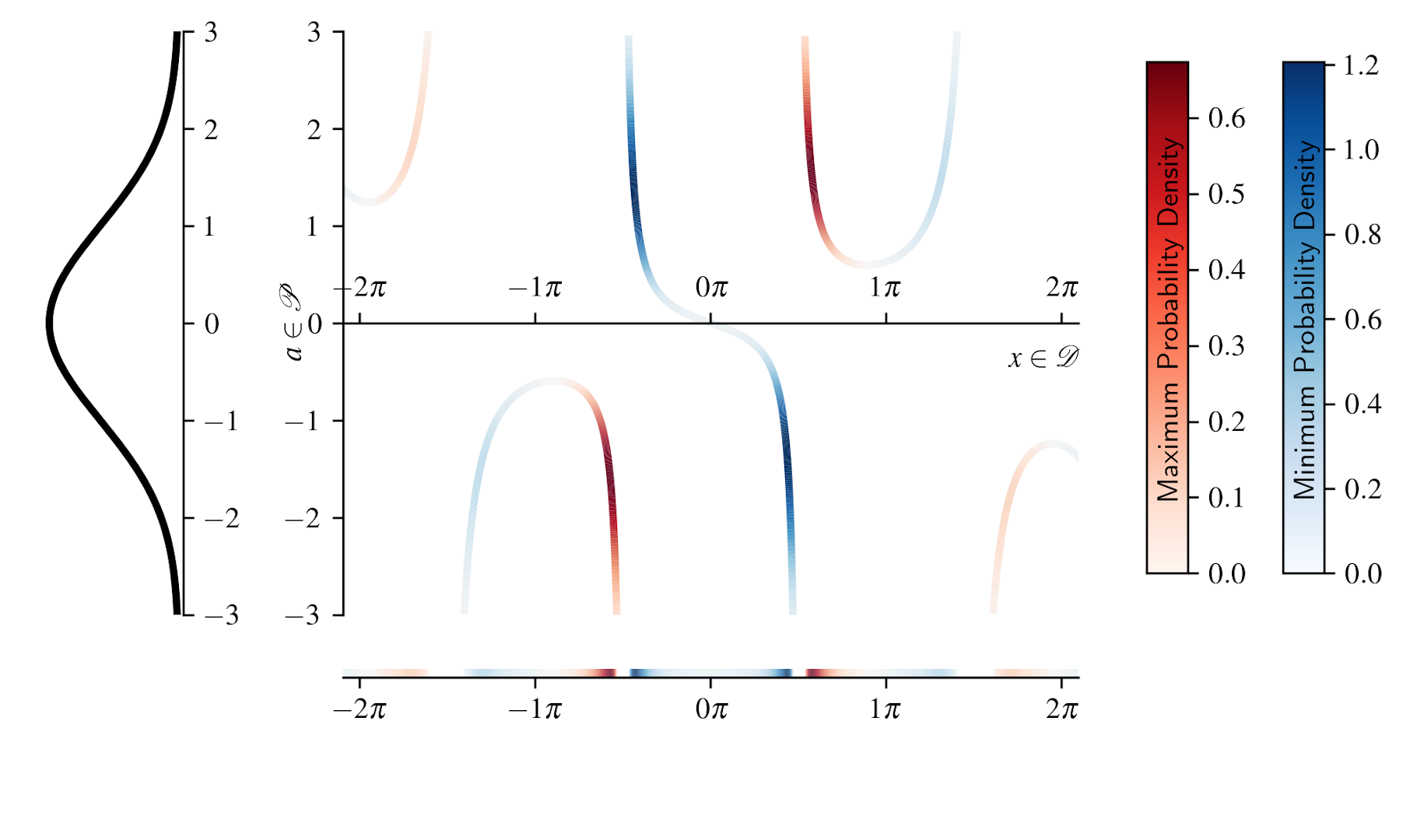
Abstract
Critical points mark locations in the domain where the level-set topology of a scalar function undergoes fundamental changes and thus indicate potentially interesting features in the data. Established methods exist to locate and relate such points in a deterministic setting, but it is less well understood how the concept of critical points can be extended to the analysis of uncertain data. Most methods for this task aim at finding likely locations of critical points or estimate the probability of their occurrence locally but do not indicate if critical points at potentially different locations in different realizations of a stochastic process are manifestations of the same feature, which is required to characterize the spatial uncertainty of critical points. Previous work on relating critical points across different realizations reported challenges for interpreting the resulting spatial distribution of critical points but did not investigate the causes. In this work, we provide a mathematical formulation of the problem of finding critical points with spatial uncertainty and computing their spatial distribution, which leads us to the notion of uncertain critical points. We analyze the theoretical properties of these structures and highlight connections to existing works for special classes of uncertain fields. We derive conditions under which well-interpretable results can be obtained and discuss the implications of those restrictions for the field of visualization. We demonstrate that the discussed limitations are not purely academic but also arise in real-world data.