Sketching Merge Trees for Scientific Visualization
Mingzhe Li, Sourabh Palande, Lin Yan, Bei Wang
Room: 106
2023-10-22T03:00:00ZGMT-0600Change your timezone on the schedule page
2023-10-22T03:00:00Z
Fast forward
Full Video
Abstract
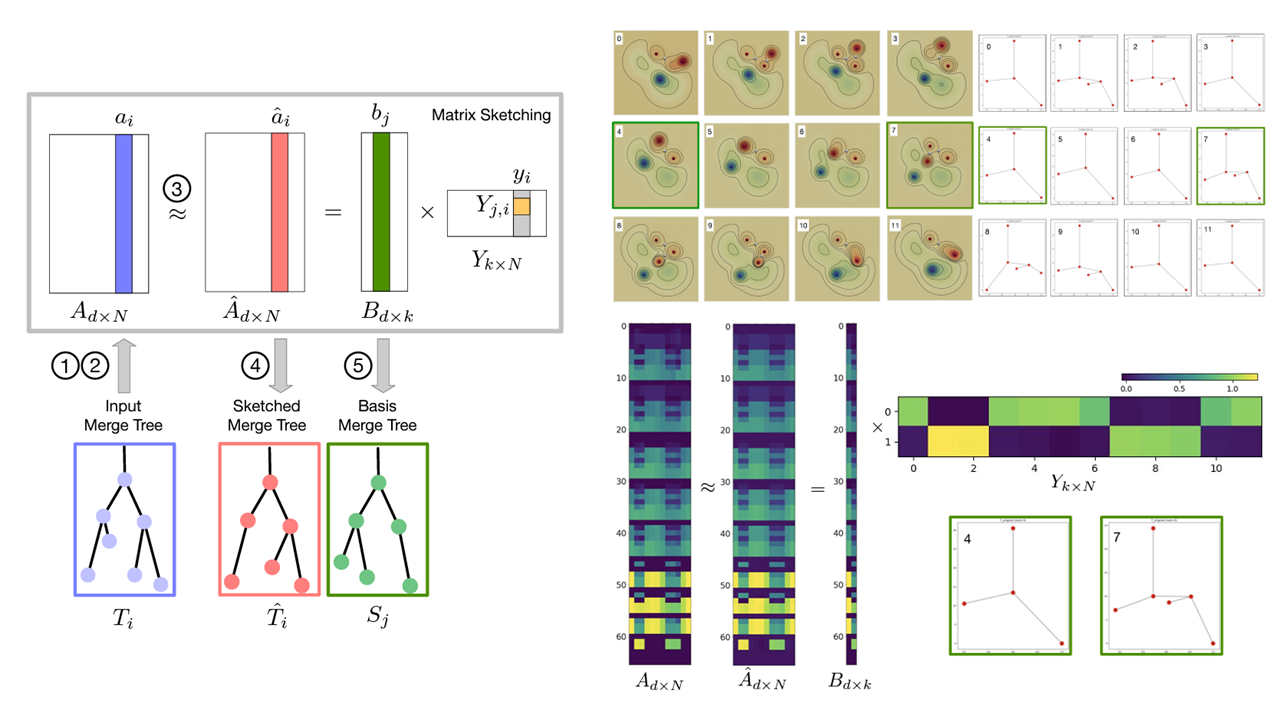
Merge trees are a type of topological descriptors that record the connectivity among the sublevel sets of scalar fields. They are among the most widely used topological tools in visualization. In this paper, we are interested in sketching a set of merge trees using techniques from matrix sketching. That is, given a large set T of merge trees, we would like to find a much smaller set of basis trees S such that each tree in T can be approximately reconstructed from a linear combination of merge trees in S. A set of high-dimensional vectors can be approximated via matrix sketching techniques such as principal component analysis and column subset selection. However, until now, there has not been any work on sketching a set of merge trees. We develop a framework for sketching a set of merge trees that combines matrix sketching with tools from optimal transport. In particular, we vectorize a set of merge trees into high-dimensional vectors while preserving their structures and structural relations. We demonstrate the applications of our framework in sketching merge trees that arise from time-varying scientific simulations. Specifically, our framework obtains a set of basis trees as representatives that capture the “modes” of physical phenomena for downstream analysis and visualization.