Combinatorial Exploration of Morse–Smale Functions on the Sphere via Interactive Visualization

Fast forward

Abstract

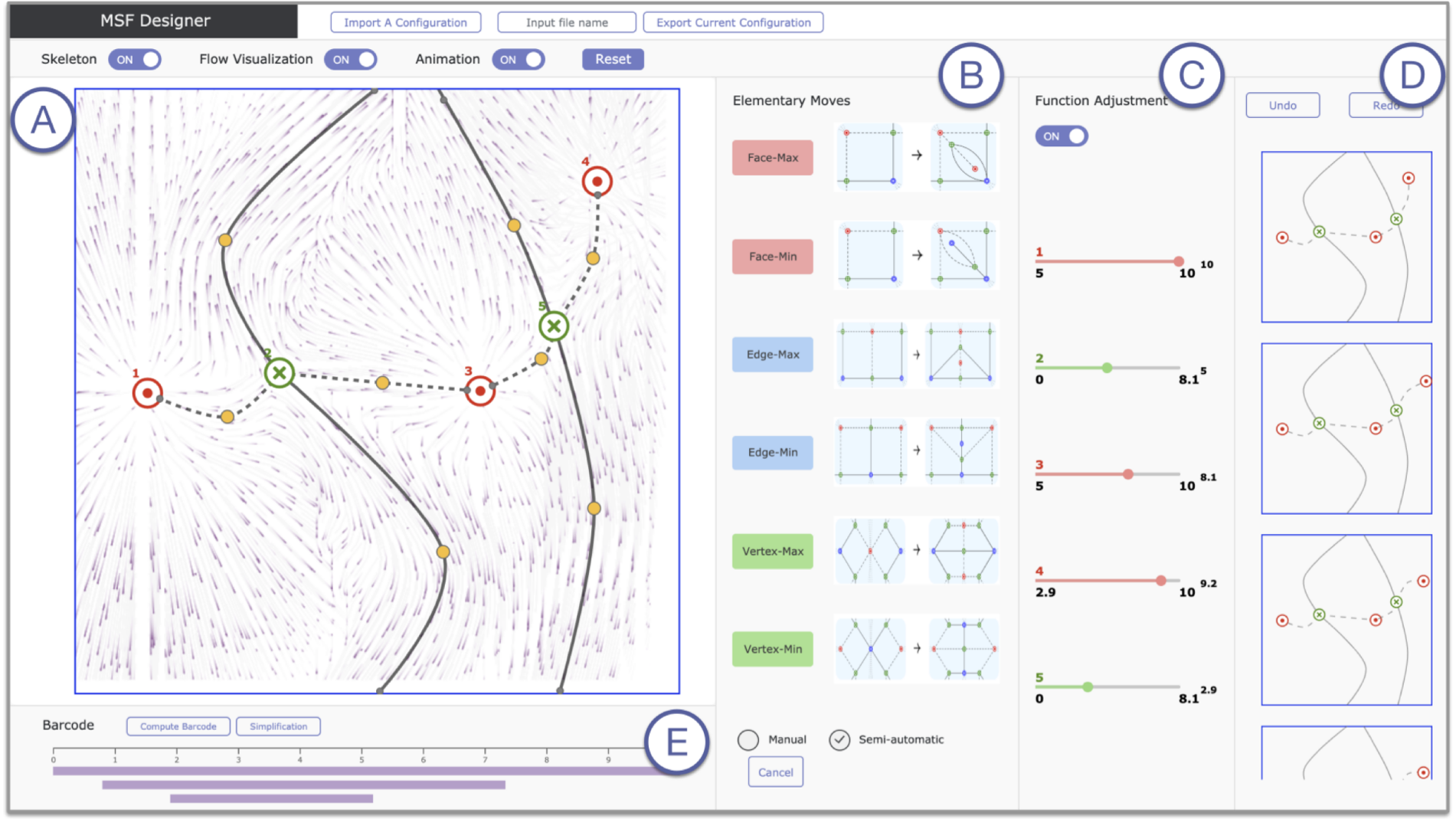
In this paper, we are interested in the characterization and classification of Morse–Smale functions. To that end, we present MSF Designer, an interactive visualization tool that supports the combinatorial exploration of Morse–Smale functions on the sphere. Our tool supports the design and visualization of a Morse–Smale function in a simple way using fundamental moves, which are combinatorial operations introduced by Catanzaro et al. that modify the Morse–Smale graph of the function. It also provides fine-grained control over the geometry and topology of its gradient vector field. The tool is designed to help mathematicians explore the complex configuration spaces of Morse–Smale functions, as well as their associated gradient vector fields and Morse–Smale complexes. Understanding these spaces will help mathematicians expand their applicability in topological data analysis and visualization. In particular, our tool helps topologists, geometers, and combinatorialists explore invariants in the classification of vector fields and characterize Morse functions in the persistent homology setting.