Topological Analysis of Ensembles of Hydrodynamic Turbulent Flows, an Experimental Study

Florent Nauleau, Fabien Vivodtzev, Thibault Bridel-Bertomeu, Héloïse Beaugendre, Julien Tierny

View presentation:2022-10-16T19:25:00ZGMT-0600Change your timezone on the schedule page
2022-10-16T19:25:00Z
Exemplar figure, described by caption below
Topological Data Analysis protocols applied on an ensemble dataset of a Kelvin-Helmholtz instability. (a) The 180 members of the ensemble obtained with variations of timesteps, interpolation schemes, orders, resolutions and Riemann solvers (Tab. 1). (b) The top cluster represents the time separation of t0 and t1 for the flows S1 and S2 with the Wasserstein distance and the bottom cluster with the L2 -norm. Red lines show the timestep separation with our clustering method whereas the sphere colors are the ground truth, illustrating the limitation of the L2 -norm. (c) Persistence curve protocol: Differences between integrals of persistence curves (gray area) of the enstrophy computed with a SLAU2 solver, an order 7 TENO scheme and a resolution of 1024 × 1024 for various configurations (S1 at t0, S2 and S3 at t1). These integral differences exhibit the appearance of vortices (critical points) as the time increases. (d) Outlier distance protocol: Wasserstein distance matrix for 5 configurations S1 (t0 , HLLC), S2 (t1 , Roe), S3 (t1 , HLLC), S4 (t2 , Roe), S5 (t2 , HLLC) computed with an order 7 WENO-Z interpolation scheme at 512 × 512. The sum of each row the configuration maximizing this distance between solvers and timesteps, here S1 . (e) Unsupervised classification: Wasserstein distance matrix for the previous configurations with an order 7 WENO-Z interpolation scheme at 256 × 256. The clustering based on the Wasserstein distance and colored according to the Kmeans clustering method successfully segments the time steps.

The live footage of the talk, including the Q&A, can be viewed on the session page, LDAV: Topology & Ensembles.

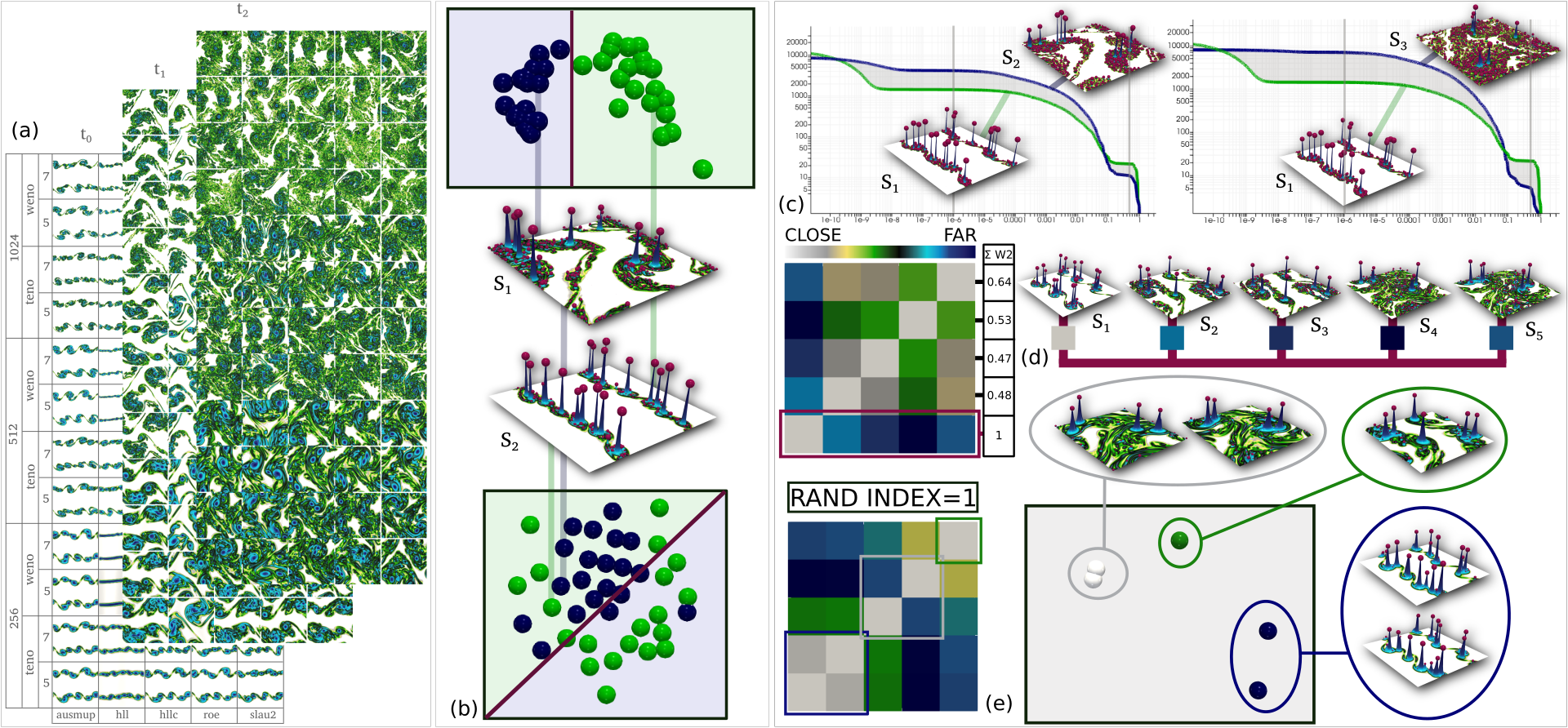
Abstract

This application paper presents a comprehensive experimental evaluation of the suitability of Topological Data Analysis (TDA) for the quantitative comparison of turbulent flows. Specifically, our study documents the usage of the persistence diagram of the maxima of flow enstrophy (an established vorticity indicator), for the topological representation of 180 ensemble members, generated by a coarse sampling of the parameter space of five numerical solvers. We document five main hypotheses reported by domain experts, describing their expectations regarding the variability of the flows generated by the distinct solver configurations. We contribute three evaluation protocols to assess the validation of the above hypotheses by two comparison measures: (i) a standard distance used in distance between persistence diagrams (the L2 -Wasserstein metric). Extensive experiments on the input ensemble demonstrate the superiority of the topological distance (ii) to report as close to each other flows which are expected to be similar by domain experts, due to the configuration of their vortices. Overall, the insights reported by our study bring an experimental evidence of the suitability of TDA for representing and comparing turbulent flows, thereby providing to the fluid dynamics community confidence for its usage in future work. Also, our flow data and evaluation protocols provide to the TDA community an application-approved benchmark for the evaluation and design of further topological distances.