Constrained Dynamic Mode Decomposition



Tim Krake, Daniel Klötzl, Bernhard Eberhardt, Daniel Weiskopf

 View presentation:2022-10-19T14:12:00ZGMT-0600Change your timezone on the schedule page
2022-10-19T14:12:00Z

Exemplar figure, described by caption below — The decomposition of time series into seasonal and trend patterns can be performed with Dynamic Mode Decomposition. The extracted DMD components capture these patterns only in an approximate fashion, although knowledge about time scales or specific periodicities is often present. Our technique, constrained Dynamic Mode Decomposition, enables incorporation of user-defined frequencies into DMD, which makes an explorative investigation of time series possible.

Prerecorded Talk

The live footage of the talk, including the Q&A, can be viewed on the session page, Temporal Data.

Fast forward

Abstract

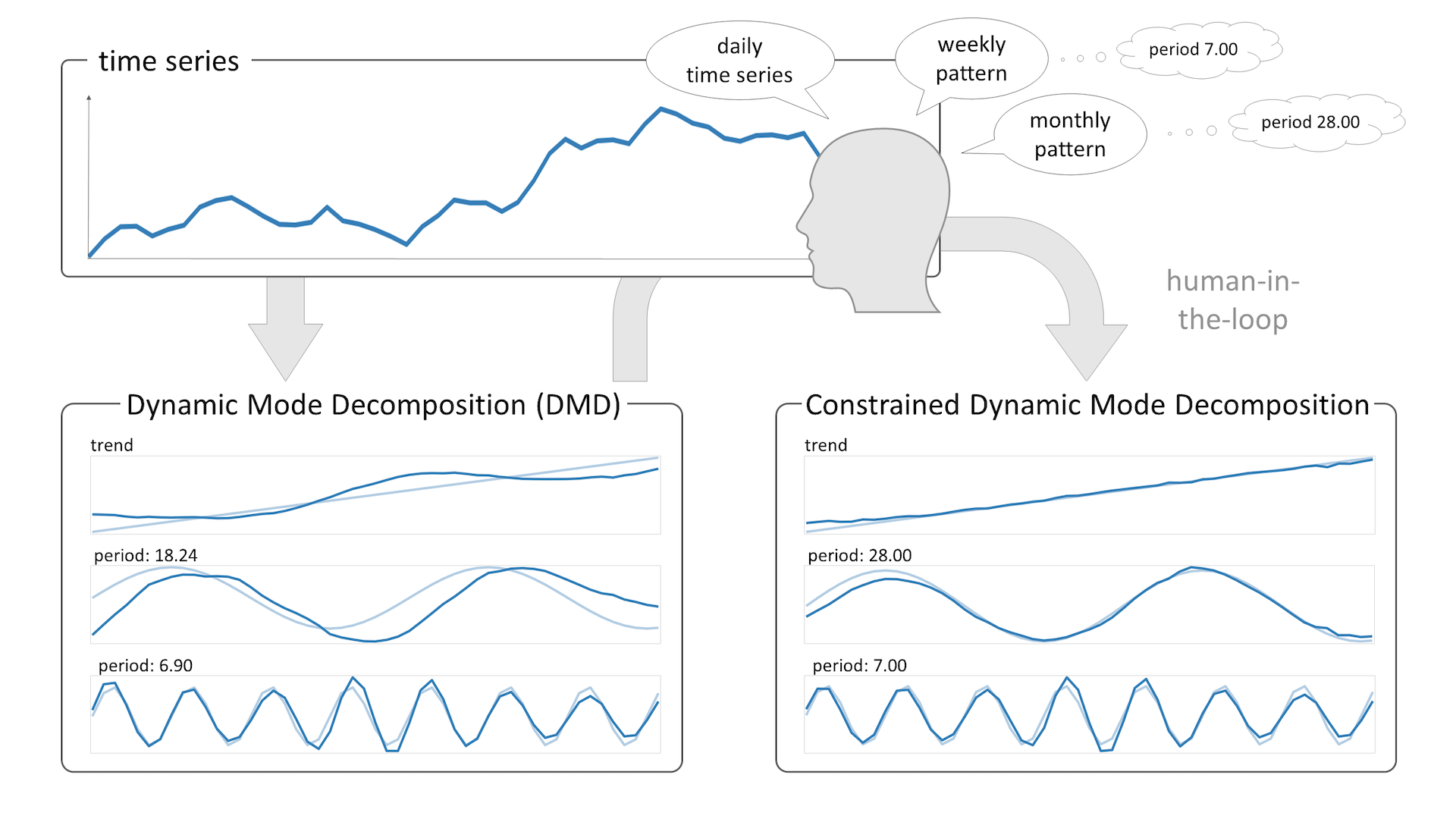
Frequency-based decomposition of time series data is used in many visualization applications. Most of these decomposition methods (such as Fourier transform or singular spectrum analysis) only provide interaction via pre- and post-processing, but no means to influence the core algorithm. A method that also belongs to this class is Dynamic Mode Decomposition (DMD), a spectral decomposition method that extracts spatio-temporal patterns from data. In this paper, we incorporate frequency-based constraints into DMD for an adaptive decomposition that leads to user-controllable visualizations, allowing analysts to include their knowledge into the process. To accomplish this, we derive an equivalent reformulation of DMD that implicitly provides access to the eigenvalues (and therefore to the frequencies) identified by DMD. By utilizing a constrained minimization problem customized to DMD, we can guarantee the existence of desired frequencies by minimal changes to DMD. We complement this core approach by additional techniques for constrained DMD to facilitate explorative visualization and investigation of time series data. With several examples, we demonstrate the usefulness of constrained DMD and compare it to conventional frequency-based decomposition methods.