Fiber Uncertainty Visualization for Bivariate Data With Parametric and Nonparametric Noise Models
Tushar M. Athawale, Chris R. Johnson, Sudhanshu Sane, David Pugmire
View presentation:2022-10-19T20:45:00ZGMT-0600Change your timezone on the schedule page
2022-10-19T20:45:00Z
Prerecorded Talk
The live footage of the talk, including the Q&A, can be viewed on the session page, Uncertainty.
Fast forward
Abstract
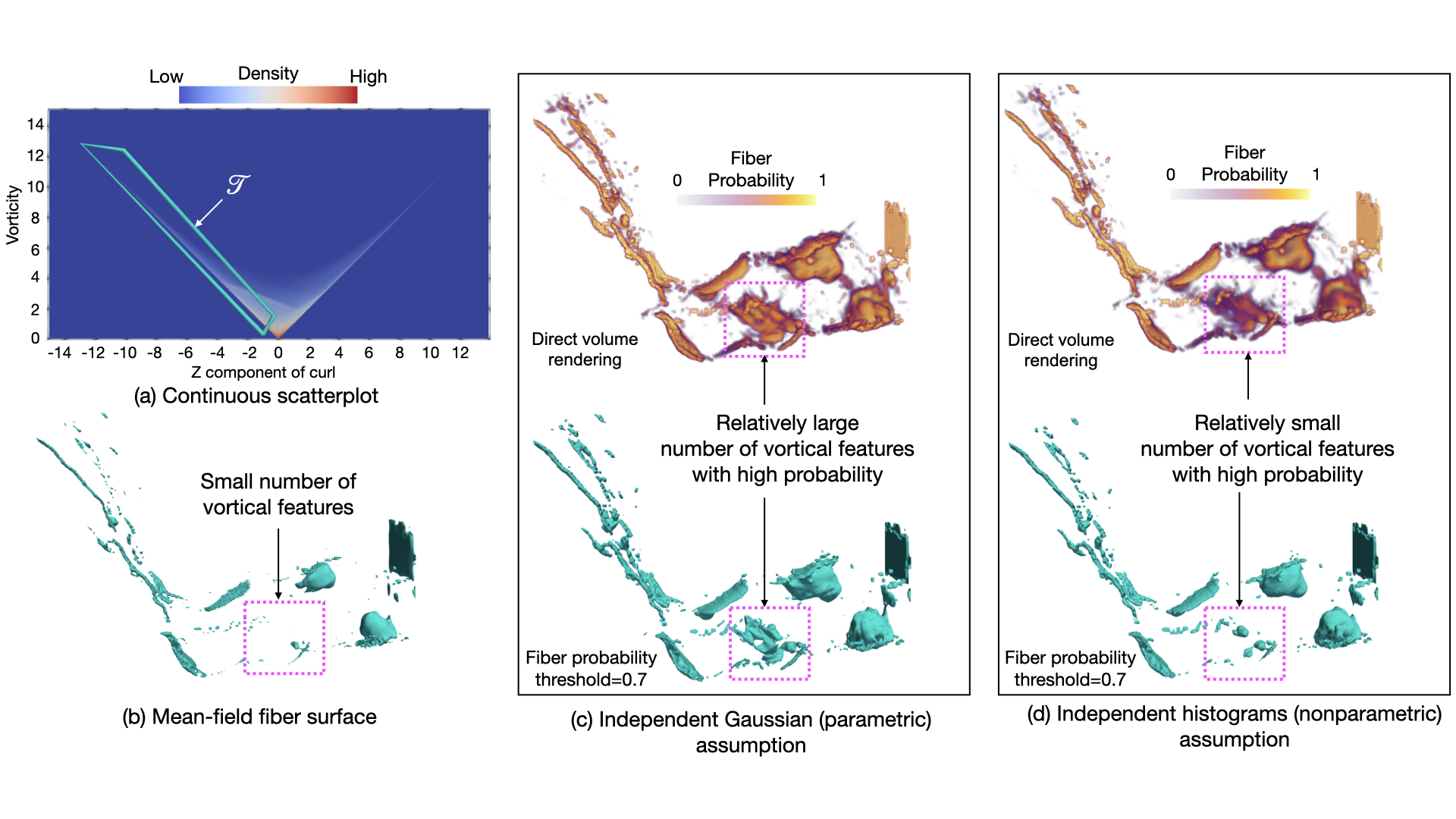
Visualization and analysis of multivariate data and their uncertainty are top research challenges in data visualization. Constructing fiber surfaces is a popular technique for multivariate data visualization that generalizes the idea of level-set visualization for univariate data to multivariate data. In this paper, we present a statistical framework to quantify positional probabilities of fibers extracted from uncertain bivariate fields. Specifically, we extend the state-of-the-art Gaussian models of uncertainty for bivariate data to other parametric distributions (e.g., uniform and Epanechnikov) and more general nonparametric probability distributions (e.g., histograms and kernel density estimation) and derive corresponding spatial probabilities of fibers. In our proposed framework, we leverage Green’s theorem for closed-form computation of fiber probabilities when bivariate data are assumed to have independent parametric and nonparametric noise. Additionally, we present a nonparametric approach combined with numerical integration to study the positional probability of fibers when bivariate data are assumed to have correlated noise. For uncertainty analysis, we visualize the derived probability volumes for fibers via volume rendering and extracting level sets based on probability thresholds. We present the utility of our proposed techniques via experiments on synthetic and simulation datasets.