Persistence cycles for visual exploration of persistent homology

Prerecorded Talk

The live footage of the talk, including the Q&A, can be viewed on the session page, Topology.

Fast forward

Keywords

Persistent homology, Topological Data Analysis, Scalar fields

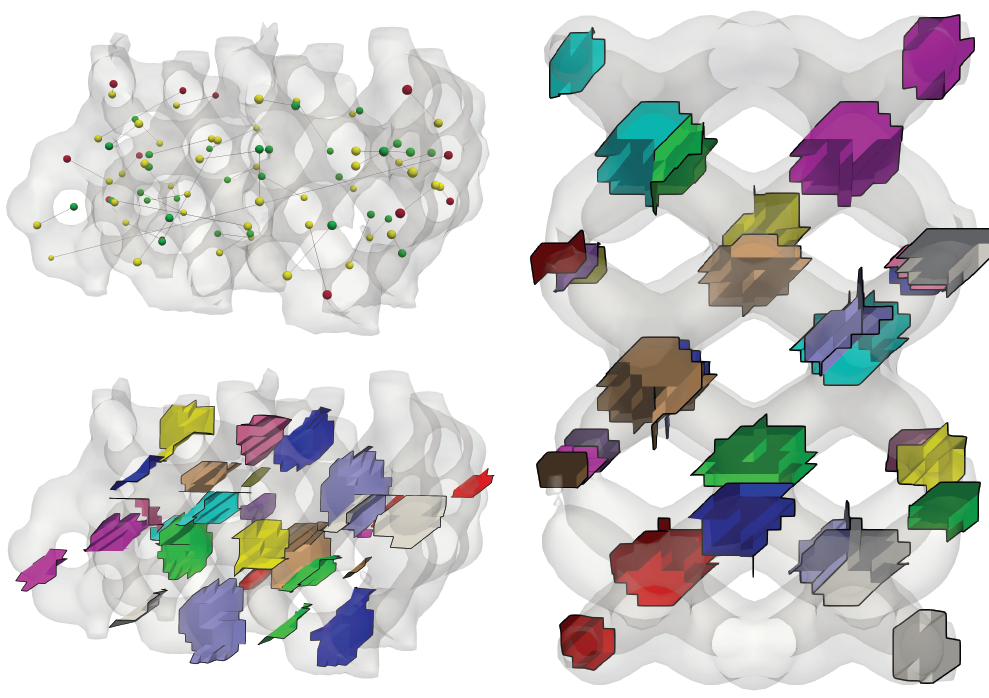
Abstract

Persistent homology is a fundamental tool in topological data analysis used for the most diverse applications. Information captured by persistent homology is commonly visualized using scatter plots representations. Despite being widely adopted, such a visualization technique limits user understanding and is prone to misinterpretation. This paper proposes a new approach for the efficient computation of persistence cycles, a geometric representation of the features captured by persistent homology. We illustrate the importance of rendering persistence cycles when analyzing scalar fields, and we discuss the advantages that our approach provides compared to other techniques in topology-based visualization. We provide an efficient implementation of our approach based on discrete Morse theory, as a new module for the Topology Toolkit. We show that our implementation has comparable performance with respect to state-of-the-art toolboxes while providing a better framework for visually analyzing persistent homology information.