Topological Simplifications of Hypergraphs



Youjia Zhou, Archit Rathore, Emilie Purvine, Bei Wang

 View presentation:2022-10-20T21:21:00ZGMT-0600Change your timezone on the schedule page
2022-10-20T21:21:00Z

Exemplar figure, described by caption below — We propose a topological simplification framework for hypergraphs, and provide an interactive tool that allows users to explore the simplification framework and apply vertex and hyperedge simplifications to gain insights from their own datasets. The image demonstrates the original hypergraph (a) from an active Domain Name System (DNS) dataset and the simplified hypergraph (c) after hyperedge simplification.

Prerecorded Talk

The live footage of the talk, including the Q&A, can be viewed on the session page, Topology.

Fast forward

Keywords

Hypergraph simplification, hypergraph visualization, graph simplification, topological data analysis

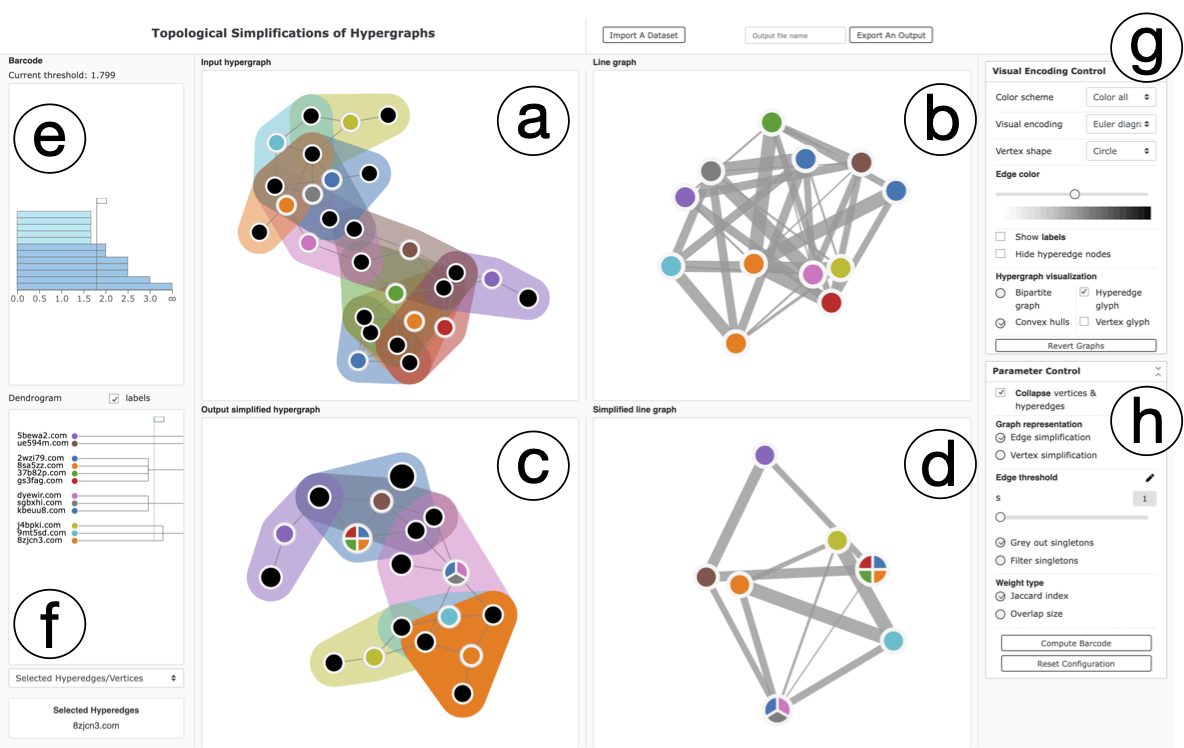
Abstract

We study hypergraph visualization via its topological simplification. We explore both vertex simplification and hyperedge simplification of hypergraphs using tools from topological data analysis. In particular, we transform a hypergraph into its graph representations known as the line graph and clique expansion. A topological simplification of such a graph representation induces a simplification of the hypergraph. In simplifying a hypergraph, we allow vertices to be combined if they belong to almost the same set of hyperedges, and hyperedges to be merged if they share almost the same set of vertices. Our proposed approaches are general, mathematically justifiable, and put vertex simplification and hyperedge simplification in a unifying framework.