Reduced Connectivity for Local Bilinear Jacobi Sets
Daniel Klötzl, Tim Krake, Youjia Zhou, Jonathan Stober, Kathrin Schulte, Ingrid Hotz, Bei Wang, Daniel Weiskopf
View presentation:2022-10-17T20:59:00ZGMT-0600Change your timezone on the schedule page
2022-10-17T20:59:00Z
The live footage of the talk, including the Q&A, can be viewed on the session page, TopoInVis: Session 2, Early Career Lightning Talks + Best Paper Awards .
Keywords
Human-centered computing - Visualization - Visualization techniques; Mathematics of computing - Discrete mathematics
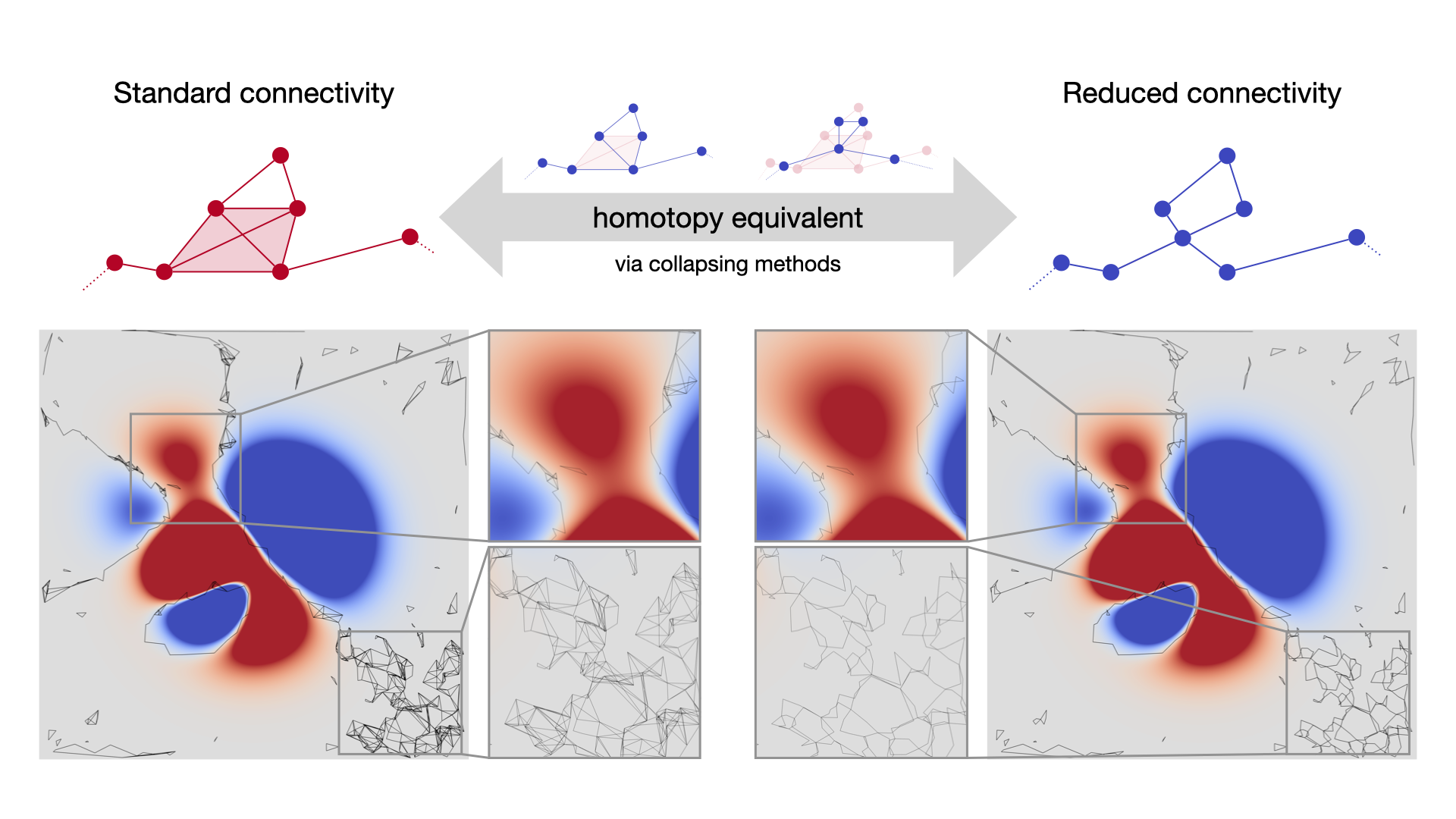
Abstract
We present a new topological connection method for the local bilinear computation of Jacobi sets that improves the visual representation while preserving the topological structure and geometric configuration. To this end, the topological structure of the local bilinear method is utilized, which is given by the nerve complex of the traditional piecewise linear method. Since the nerve complex consists of higher-dimensional simplices, the local bilinear method (visually represented by the 1-skeleton of the nerve complex) leads to clutter via crossings of line segments. Therefore, we propose a homotopy-equivalent representation that uses different collapses and edge contractions to remove such artifacts. Our new connectivity method is easy to implement, comes with only little overhead, and results in a less cluttered representation.