A Deformation-based Edit Distance for Merge Trees

The live footage of the talk, including the Q&A, can be viewed on the session page, TopoInVis: Session 2, Early Career Lightning Talks + Best Paper Awards .

Keywords

Scalar data, Topological data analysis, Merge trees, Edit distance

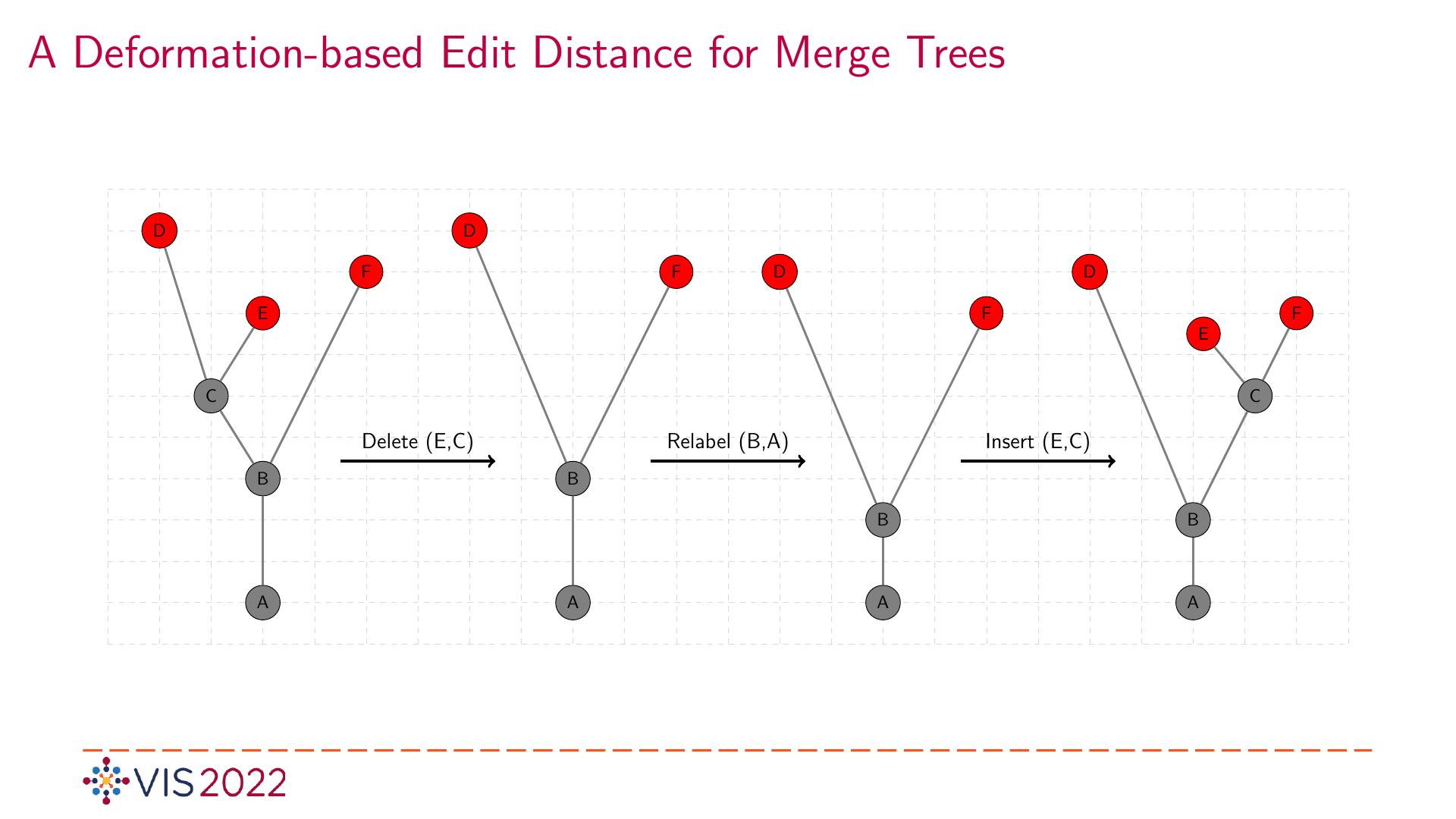
Abstract

In scientific visualization, scalar fields are often compared through edit distances between their merge trees. Typical tasks include ensemble analysis, feature tracking and symmetry or periodicity detection. Tree edit distances represent how one tree can be transformed into another through a sequence of simple edit operations: relabeling, insertion and deletion of nodes. In this paper, we present a new set of edit operations working directly on the merge tree as an geometrical or topological object: the represented operations are deformation retractions and inverse transformations on merge trees, which stands in contrast to other methods working on branch decomposition trees. We present a quartic time algorithm for the new edit distance, which is branch decomposition-independent and a metric on the set of all merge trees.